Decimal to number system conversion
To convert a decimal number system to a binary number system division method is used. The given Decimal number is divided by 2 until the quotient is less than 2. To convert the fraction number to binary multiply the fraction with the base (2) to get a new integer and a fraction. Remove the integer from the result and the multiplication with the new fraction is repeated till the result becomes zero.
Example 1: (25)10 = () 2

2510 = 110012
Example 2: (34.45)10 = (?)2
Whole number Part:
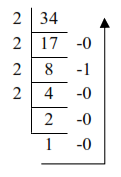
3410 = 1000102
Decimal Part:
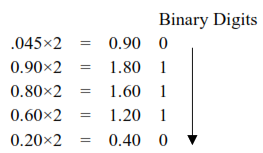
0.4510=0.011102
The bunary equivallent of (34.45)10= (100010.01110)2
Decimal to Octal number system conversion
To convert a decimal number system to an Octal number system division method is used. The given
Decimal number is divided by octal number system’s base 8 until the quotient is less than 8. To convert the fraction number to octal multiply the fraction with the base of octal number (8) to get a new integer and a fraction. Remove the integer from the result and the multiplication with the new fraction is repeated till the result becomes zero.
Example 3: (144.25)10 = (?)8
Whole number Part:
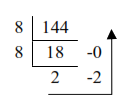
14410 = 2208
Decimal Part:

0.2510=0.208
(144.25)10= (220.20)8
Decimal to Hexadecimal number system conversion
To convert a decimal number system to a Hexadecimal number system division method is used. The given Decimal number is divided by 16 until the quotient is less than 16. To convert the fraction number to Hexadecimal multiply the fraction with the base of hexadecimal number (16) to get a new integer and a fraction. Remove the integer from the result and the multiplication with the new fraction is repeated till the result becomes zero.
Example 4: (100)10 = (?)16

10010 = 6416
Binary to Decimal number system conversion
To convert a Binary number system to Decimal number system multiplication method is used. The given binary number is multiplied by the increasing powers of 2 based on the bit position
Example 6: (110110)2 = (?)10
Graphical Method:

Equation Method:
= 0 × 20 + 1 × 21 + 1 × 22 + 0 × 23 + 1 × 24 + 1 × 25
= 0 + 2 + 4 + 0 + 16 + 32
= 54
∴ (110110)2 = (54)10
Example 7: (11110.0101)2 = (?)10
Graphical Method:
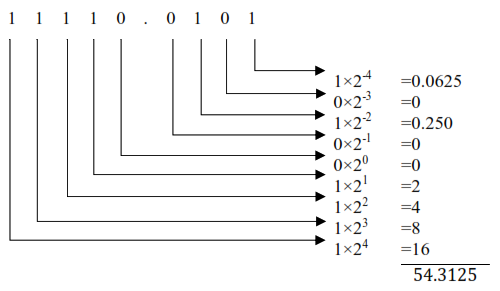
Equation Method:
=1×2-4 + 0×2-3 + 1×2-2 + 0×2-1 + 0×20 + 1×21 +1×22 +1×23 +1×24
=0.0625+0+0.250+0+0+2+4+8+16
=54.3125
∴ (11110.0101)2 = (54.3125)10
Binary to Octal number system conversion
To convert a Binary number system to octal number system the given binary number is split into three bit groups. For this group the equivalent octal values are written
Example 8: (11110101.0101110)2 = (?)8

Binary to Hexadecimal number system conversion
To convert a Binary number system to Hexadecimal number system the given binary number is split into four bit groups. For this group the equivalent octal values are written
Example 9: (11110101.0101110)2 = (?)16

(11110101.0101110)2 = (F5.5C)16
Octal to Binary number system conversion
To convert the octal number system to binary system represent the values of each octal number as a three bit binary number. Example 10: (7405)8 = (?)2

(7405)8 = (111100000101)2
Example 11: (627.35)8 = (?)2

(627.35)8 = (110010111011101)2
Hexadecimal to Binary number system conversion
To convert Hexadecimal number system to binary system represents the values of each Hexadecimal number as four bit binary number.
Example 12: (F405)8 = (?)2

(F405)8 = (1111010000000101)2
Example 13: (ACF.E1)8 = (?)2
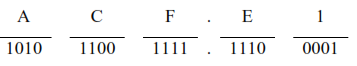
(ACF.E1)16 = (101011001111.11100001)2
Octal to Hexadecimal number system conversion
Convert the octal number to binary. Split the binary number into four bits and represent the equivalent hexadecimal system
Example 14: (405)8 = (?)16

(405)8 = (100000101)2
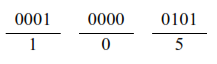
(405)8 = (105)16





